I've had several projects over the past few years that required small, specific reduction gears, and I've always designed and printed the required parts, with varying degrees of success. Gears are not the easiest of parts to make. Increasingly I find that the best practices of software engineering apply beautifully for CAD engineering, so following one of the rules of functionalization, if you write it more than three times, then you should probably turn it into a standalone function. It was time to make gears for their own sake based on the expectation that it would save me time in the future. Like I said, there's quite a bit of geometry and physics theory that goes into high performance gear design. It's not just putting sticks on the outside of a wheel. In the past I had learned just enough of this theory so that I was able to make Solidworks parts that would work for that day's application but were not repurposable for future use. So today's goal is to learn a bit more of the theory and produce a single Solidworks part file that can easily produce more or less any gear required in the future.
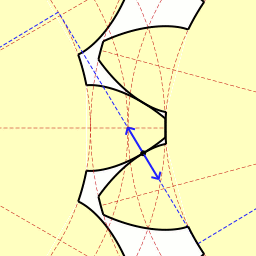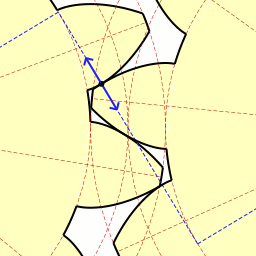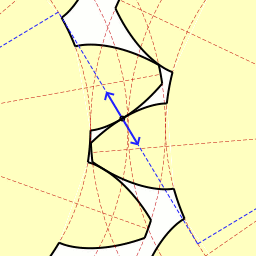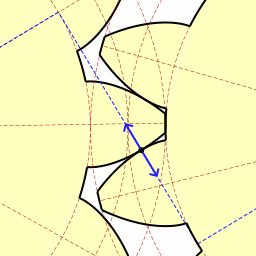
There are at least two geometric principles that must be understood to design optimal gear teeth: the Involute Curve profile and Pressure Angles. The involute curve is a solution to the problem of how gear teeth should interact with each other. Ideally, two teeth should not collide violently at a sharp corner, but should roll smoothly across each other, like a wheel rolling smoothly across a flat floor. The involute curve is created by peeling a point away from the surface of a wheel. Take a cylindrical object, something like a soup can, wrap a string around it, and then tie the outer end of the string around a pencil. If you unwrap the string, keeping the string taut, and draw the curve produced, then the curve drawn is an involute curve. Here's a video explanation.
If you make a gear tooth that is shaped like an involute curve, then instead of scraping against each other at a sharp corner, the gear teeth will roll smoothly and continuously across each other, across the entire tooth face, producing a smooth and continuous transmission of force with minimal friction.
So this tells us how our teeth should be shaped, but not how they should be positioned relative to one another. That is determined by the Pressure Angle. Formally, the pressure angle is the angle between the line that is tangent to both pitch circles and the line that is tangent to both base circles. Practically, the pressure angle is the angle between the contact between gears and the contact between gear teeth.
As pressure angle increases, your contacts between gear teeth become slower and smoother, meaning your overall gear motion becomes smoother, but more energy goes into compression of gear teeth and it becomes easier for gear teeth to slip with respect to one another, so your gears can transmit smaller torques before slipping and must be manufactured with higher precision. Here's a video that illustrates all of the geometry terms I just used.
Combining the involute profile and the pressure angle, our end result is a gear tooth that has an involute curve outside the base circle and a flat face inside the base circle (You should actually use a curved face below the base circle to prevent interference, but our gears are small enough and soft enough that that won't matter). So as your pressure angle or number of gear teeth decrease, your teeth become taller, thinner, and straighter. As pressure angle or number of teeth increase, the base circle drops inside the bottom of the gear teeth and the teeth become nothing but an involute curve, with no flat face at the bottom. Understanding all of these concepts together, it's possible to produce a single Solidworks part that can produce just about any gear required.
Our file starts with a list of equations and user-specified values for number of teeth, tooth pitch, tooth height, gear wall thickness, tooth skew, and several other variables. In practice, number of teeth is the only variable I expect to change on a regular basis. Then we draw a sketch that contains everything, our gear body and all of the circles and angles and curves required to define a single perfect tooth. We then extrude the gear body, then extrude a single tooth, then pattern that tooth, and then cut holes in the body to reduce mass and printing time. If that first sketch is properly constrained, then we should be able to change any of the user-specified constants without changing anything else in the part.
So here it is, our finished Solidworks part files, one for Spur gears and one for Herringbone gears. Herringbone are superior to Spur for most purposes. Herringbones have multiple teeth in contact at all times along a skewed axis, so they produce much smoother motion. They are much more complex to produce using cutting methods, but a printer doesn't care. To modify, we simply open the Equations table and change whatever we want to change, then save as an STL and print.
I haven't found any problems related to solving new combinations of parameters. If anyone uses this and does find problems, please let me know. This should mean that I never have to design a 3D printed gear again.
All files, Solidworks and generic STL, are available on GradCAD.
If you make a gear tooth that is shaped like an involute curve, then instead of scraping against each other at a sharp corner, the gear teeth will roll smoothly and continuously across each other, across the entire tooth face, producing a smooth and continuous transmission of force with minimal friction.
As pressure angle increases, your contacts between gear teeth become slower and smoother, meaning your overall gear motion becomes smoother, but more energy goes into compression of gear teeth and it becomes easier for gear teeth to slip with respect to one another, so your gears can transmit smaller torques before slipping and must be manufactured with higher precision. Here's a video that illustrates all of the geometry terms I just used.
Combining the involute profile and the pressure angle, our end result is a gear tooth that has an involute curve outside the base circle and a flat face inside the base circle (You should actually use a curved face below the base circle to prevent interference, but our gears are small enough and soft enough that that won't matter). So as your pressure angle or number of gear teeth decrease, your teeth become taller, thinner, and straighter. As pressure angle or number of teeth increase, the base circle drops inside the bottom of the gear teeth and the teeth become nothing but an involute curve, with no flat face at the bottom. Understanding all of these concepts together, it's possible to produce a single Solidworks part that can produce just about any gear required.
Our file starts with a list of equations and user-specified values for number of teeth, tooth pitch, tooth height, gear wall thickness, tooth skew, and several other variables. In practice, number of teeth is the only variable I expect to change on a regular basis. Then we draw a sketch that contains everything, our gear body and all of the circles and angles and curves required to define a single perfect tooth. We then extrude the gear body, then extrude a single tooth, then pattern that tooth, and then cut holes in the body to reduce mass and printing time. If that first sketch is properly constrained, then we should be able to change any of the user-specified constants without changing anything else in the part.
So here it is, our finished Solidworks part files, one for Spur gears and one for Herringbone gears. Herringbone are superior to Spur for most purposes. Herringbones have multiple teeth in contact at all times along a skewed axis, so they produce much smoother motion. They are much more complex to produce using cutting methods, but a printer doesn't care. To modify, we simply open the Equations table and change whatever we want to change, then save as an STL and print.
|
|
|
I haven't found any problems related to solving new combinations of parameters. If anyone uses this and does find problems, please let me know. This should mean that I never have to design a 3D printed gear again.
All files, Solidworks and generic STL, are available on GradCAD.